Throughout this post,  is a ring with identity and
is a ring with identity and 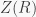 is its center. We denote by
is its center. We denote by  the set of idempotents of
the set of idempotents of  i.e.
i.e. 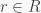 such that
such that  Also,
Also, ![R[x]](https://s0.wp.com/latex.php?latex=R%5Bx%5D&bg=f9f9f9&fg=333333&s=0&c=20201002) is the ring of polynomials in
is the ring of polynomials in  with coefficients in
with coefficients in 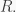 Given
Given 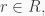 the left-multiplication map
the left-multiplication map  is defined by
is defined by  for all
for all 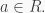 Finally, ring homomorphisms in this post are not required to preserve the identity element.
Finally, ring homomorphisms in this post are not required to preserve the identity element.
Left multiplication maps  are clearly right
are clearly right  -module homomorphisms, i.e.
-module homomorphisms, i.e.  for all
for all 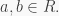 But for which
But for which 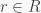 is the map
is the map  a ring homomorphism? That’s probably not easy to answer in general, but I’m going to share some of my findings with you anyway. Before I do that, let me define a class of rings with a funny name which are related to our question.
a ring homomorphism? That’s probably not easy to answer in general, but I’m going to share some of my findings with you anyway. Before I do that, let me define a class of rings with a funny name which are related to our question.
Definition. A ring  is called abelian if
is called abelian if  i.e. every idempotent of
i.e. every idempotent of  is central.
is central.
Commutative rings are clearly abelian but abelian rings are not necessarily commutative. For example, by Remark 3 in this post, every reduced ring is abelian (in fact, by Exercise 1 in that post, every reversible ring is abelian). Part vi) of the following problem gives an equivalent definition of abelian rings: a ring  is abelian if and only if
is abelian if and only if  is a ring homomorphism for every idempotent
is a ring homomorphism for every idempotent  of
of 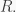
Problem (Y. Sharifi). Let  be a ring, and consider the set
be a ring, and consider the set

Show that
i) 
ii) if  is commutative, then
is commutative, then 
iii)  is multiplicatively closed,
is multiplicatively closed,
iv) given 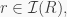 the set
the set  is a subring of
is a subring of 
v) 
vi)  if and only if
if and only if  is abelian,
is abelian,
vii) if  is semiprime, then
is semiprime, then 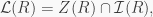
viii) if  is prime, then
is prime, then 
ix) ![\mathcal{L}(R) =R \cap \mathcal{L}(R[x])](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BL%7D%28R%29+%3DR+%5Ccap+%5Cmathcal%7BL%7D%28R%5Bx%5D%29&bg=f9f9f9&fg=333333&s=0&c=20201002) and if
and if  is commutative or semiprime, then
is commutative or semiprime, then ![\mathcal{L}(R[x])=\mathcal{L}(R),](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BL%7D%28R%5Bx%5D%29%3D%5Cmathcal%7BL%7D%28R%29%2C&bg=f9f9f9&fg=333333&s=0&c=20201002)
x)  for any family of rings
for any family of rings 
Solution. i) Since  is clearly additive, it is a ring homomorphism if and only if
is clearly additive, it is a ring homomorphism if and only if  i.e.
i.e.  for all
for all 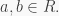 Choosing
Choosing  gives
gives  Conversely, if
Conversely, if 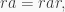 then
then  and so
and so  is a ring homomorphism.
is a ring homomorphism.
ii) By i),  if and only if
if and only if 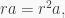 for all
for all 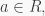 which holds if and only if
which holds if and only if 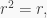 i.e
i.e 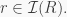
iii) Let 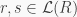 and
and 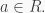 Then, by i),
Then, by i),  and so
and so  Thus
Thus 
iv) If  then
then  and so
and so 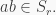
v) Let 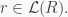 Then choosing
Then choosing 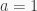 in i) gives
in i) gives  and so
and so 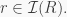 Now, let
Now, let  and
and 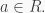 Then
Then  and so
and so 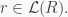
vi) If  then
then  by v). Suppose now that
by v). Suppose now that  and
and 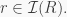 Then
Then  and so, by i),
and so, by i),  for all
for all 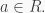 Thus
Thus

which gives 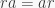 and so
and so 
vii) By v), we only need to show that  So let
So let  and
and 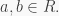 If we show that
If we show that  we are done because that means
we are done because that means  and so, since
and so, since  is semiprime,
is semiprime, 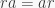 hence
hence  Now, to show that
Now, to show that  we have
we have

and so, since by i),  we get that
we get that

viii) Clearly the inclusion  holds for any ring
holds for any ring 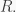 Now, suppose that
Now, suppose that  is a prime ring and
is a prime ring and  Then, by i),
Then, by i), 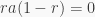 and so
and so  which gives
which gives 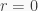 or
or 
ix) Let 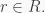 Then, by i),
Then, by i), ![r \in \mathcal{L}(R[x])](https://s0.wp.com/latex.php?latex=r+%5Cin+%5Cmathcal%7BL%7D%28R%5Bx%5D%29&bg=f9f9f9&fg=333333&s=0&c=20201002) if and only if
if and only if  for all
for all ![f(x) \in R[x]](https://s0.wp.com/latex.php?latex=f%28x%29+%5Cin+R%5Bx%5D&bg=f9f9f9&fg=333333&s=0&c=20201002) if and only if
if and only if  for all
for all 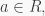 because
because  is central in
is central in ![R[x],](https://s0.wp.com/latex.php?latex=R%5Bx%5D%2C&bg=f9f9f9&fg=333333&s=0&c=20201002) if and only if
if and only if  by i).
by i).
If  is commutative, then
is commutative, then 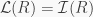 and so, since the polynomial ring
and so, since the polynomial ring ![R[x]](https://s0.wp.com/latex.php?latex=R%5Bx%5D&bg=f9f9f9&fg=333333&s=0&c=20201002) is commutative too,
is commutative too,
![\mathcal{L}(R[x])=\mathcal{I}(R[x])=\mathcal{I}(R)=\mathcal{L}(R).](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BL%7D%28R%5Bx%5D%29%3D%5Cmathcal%7BI%7D%28R%5Bx%5D%29%3D%5Cmathcal%7BI%7D%28R%29%3D%5Cmathcal%7BL%7D%28R%29.&bg=f9f9f9&fg=333333&s=0&c=20201002)
Note that the identity ![\mathcal{I}(R[x])=\mathcal{I}(R)](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BI%7D%28R%5Bx%5D%29%3D%5Cmathcal%7BI%7D%28R%29&bg=f9f9f9&fg=333333&s=0&c=20201002) is true by this post.
is true by this post.
Now suppose that  is semiprime, and
is semiprime, and ![f(x)=\sum_{i=0}^nr_ix^i \in \mathcal{L}(R[x]), \ n \ge 1.](https://s0.wp.com/latex.php?latex=f%28x%29%3D%5Csum_%7Bi%3D0%7D%5Enr_ix%5Ei+%5Cin+%5Cmathcal%7BL%7D%28R%5Bx%5D%29%2C+%5C+n+%5Cge+1.&bg=f9f9f9&fg=333333&s=0&c=20201002) So
So  for all
for all 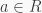 and hence, equating the coefficients of
and hence, equating the coefficients of  on both sides of the equality gives
on both sides of the equality gives  Thus
Thus  and so, since
and so, since  is semiprime,
is semiprime, 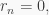 contradiction. This proves that
contradiction. This proves that 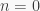 and hence
and hence  giving
giving ![\mathcal{L}(R[x]) = \mathcal{L}(R).](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BL%7D%28R%5Bx%5D%29+%3D+%5Cmathcal%7BL%7D%28R%29.&bg=f9f9f9&fg=333333&s=0&c=20201002)
x) Clear, by i). 
Example 1. This example shows that  is not always central. Let
is not always central. Let 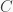 be a commutative domain, and let
be a commutative domain, and let  be the ring of
be the ring of 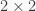 upper triangular matrices with entries in
upper triangular matrices with entries in  Then, using the first part of the Problem, it is easy to see that
Then, using the first part of the Problem, it is easy to see that

Example 2. Let  be the ring in Example 1. Then
be the ring in Example 1. Then ![\mathcal{L}(R[x]) \neq \mathcal{L}(R)](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BL%7D%28R%5Bx%5D%29+%5Cneq+%5Cmathcal%7BL%7D%28R%29&bg=f9f9f9&fg=333333&s=0&c=20201002) because
because ![f(x)=r+sx \in \mathcal{L}(R[x]),](https://s0.wp.com/latex.php?latex=f%28x%29%3Dr%2Bsx+%5Cin+%5Cmathcal%7BL%7D%28R%5Bx%5D%29%2C&bg=f9f9f9&fg=333333&s=0&c=20201002) where
where

Example 3. If  is a semisimple ring, then
is a semisimple ring, then 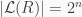 for some positive integer
for some positive integer 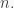
Proof. By the Artin-Wedderburn theorem,  is a finite direct product of matrix rings over division rings. The result now follows from parts viii) and x) of the Problem.
is a finite direct product of matrix rings over division rings. The result now follows from parts viii) and x) of the Problem. 
with identity, we denote by
the Jacobson radical of
the group of units of
the ring of
matrices with entries from
and the group of units of
respectively.
is a finite field, then
is a finite ring with identity, then
to find
for any finite commutative ring with identity
be a finite commutative ring with identity, and let
be the set of all maximal ideals of
Let
Then
By the Chinese Remainder Theorem,
and so, by
applied to
and also by
be the prime factorization of an integer
Then
The maximal ideals of
are
and
Also
and so
The result now follows from the Theorem.